 その7
撹拌Re数の本質を知ろう
その7
撹拌Re数の本質を知ろう
前回、 前々回の講座では、 撹拌槽内の流れのおおよその状態がレイノルズ数(Re数)と動力変化の度合いから予想できることをお話ししてきました。 今回はちょっと一休みして、 「そもそも撹拌Re数って何なのか?」に関してのお話です。
本来、 Re数は撹拌固有の特性値ではなく、 配管等での圧力損失を検討する際に用いる流体力学での「円管内流体摩擦係数とRe数の相関図」等で有名な指標です。 学生時代には、 社会生活で使わないであろう記号ベスト10に入るものと確信していましたが、 実は結構大事な指標なのですよ。
さて、 Re数の一般的な定義式は以下の通りです。

おっと、 ここで再び、 マックス君とナノ先輩の登場です。 ナノ先輩から二つほど質問が出ました。

ナノ先輩
この式の中にある代表長さや代表速度の「代表」ってどういう意味なの?何か、曖昧じゃない?

マックス君
学校の授業で習った「代表」とは、「考えたい流れの場で、最も流れに大きく影響のあると考えられる長さや速度」ということでした。円管内の流れでは、代表長さDは配管内径、代表速度Uは配管内平均流速です。代表長さを配管の全長ではなく内径としている理由は、配管内壁面での摩擦抵抗が流れに大きく影響するからだと習いました。

なるほど。最も影響度の大きいものを「代表」としているってことだね。じゃあ、動粘度ν(ニュー)ってなに?撹拌でよく使う粘度μ(ミュー:Pa・s)と何が違うの?面倒だから、普通の粘度μだけでいいんじゃないの?

うっ、動粘度と粘度の違いですか?えーっと…(学生時代のテキストを見ながら…)動粘度の定義式では以下のようになっていますね。
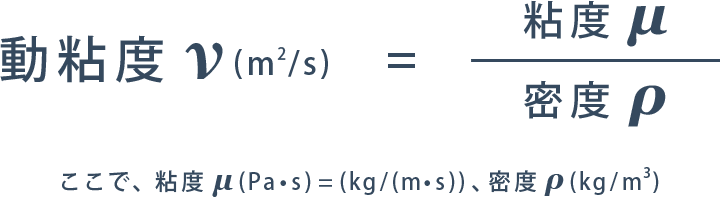

撹拌等で使われる粘度μとは、対象となる流体の性質としての粘度であり、「流体中の物体の動きにくさを表す指標」なんです。一方、動粘度νとは、「流体そのものの動きにくさを表す指標」だと書いてありますね。この流体の動きにくさに影響を及ぼすものが密度であり、同じ粘度の流体でも密度が異なればその流体の動きにくさ(動粘度)は変わるのだと。
うーん。 なかなかうまくイメージしてもらうのが難しいですね。
たとえば、 大きさの等しい鉄球とピンポン玉の表面にベトベトのオイルを塗って、 大きさが等しく同じ粘度μの物体(重さだけが異なる)を作ったとします。 表面の粘度は同じですが、 どちらが転がり易いかと言えば重量の重い(密度の大きい)鉄球になります。 これを動きやすさ(動粘度)として評価しているようです。
歯車などに使用される潤滑用オイルの品番が動粘度で示されているのも、 歯車にまとわりつく流体の動きやすさ(垂れやすさ)を評価しているのかもしれませんね。
さて、 広義のRe数の定義は理解できましたが、 まだナノ先輩には疑問が残る様子です。

なるほど。動粘度についてもなんとなく理解できたよ。でも、円管内と撹拌ではRe数の定義式の形が少し違っているように見えるんだけど…

そうですね、図1に示すように、円管内と撹拌ではRe数の代表長さと代表速度に違いがあります。
図1 円管内と撹拌のRe数
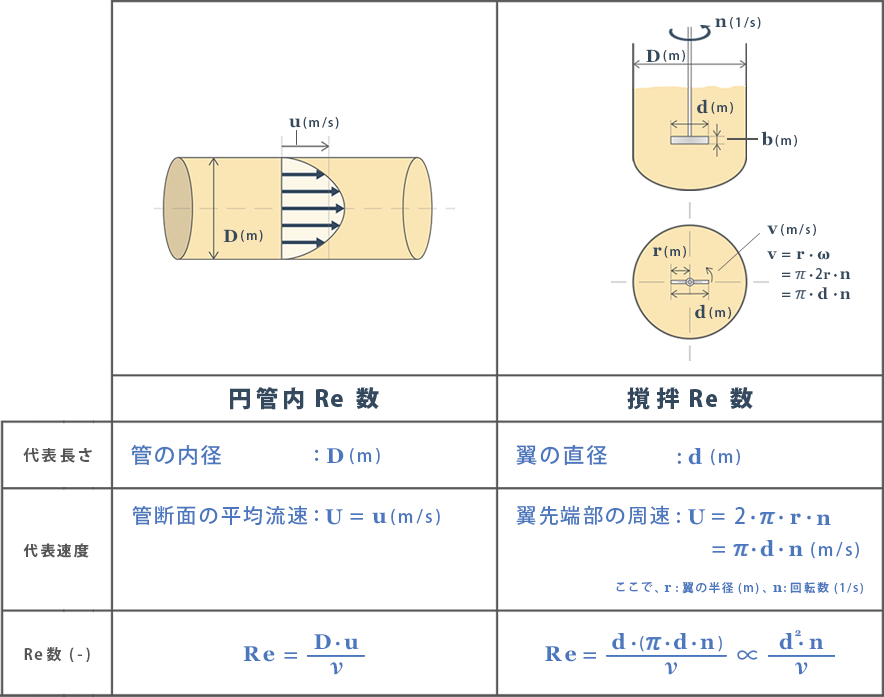

円管内の場合は、代表長さも代表速度も比較的妥当な選定と言えますが、撹拌の場合はどうでしょうか。代表長さが「撹拌翼の直径:d」、代表速度が「撹拌翼先端部の周速:U」であり、撹拌槽内の流れというよりも、どちらかと言えば、撹拌翼先端近傍の流れが主体になっている気がしますね。

確かに。そうすると、図2のように、パドル翼の1段、2段、3段、更にはマックスブレンド®翼のような大型翼を比較した場合、翼径と回転数が同一であれば4ケースとも同じ撹拌Re数になってしまうね。でも、現場で見た実際の液の流れの状況はかなり異なっている。また、消費動力も各々異なっているのでこの4ケースが同じ流れの状況とはとてもじゃないけれど思えないのだけれど…
図2 同一Re数でも、 槽内流動は異なる
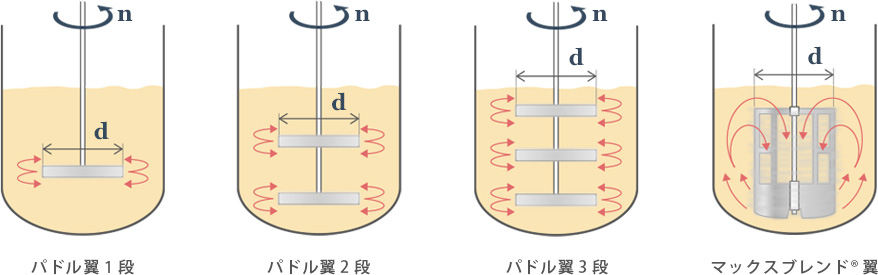

そうです!そこが撹拌Re数を使用する場合に気をつけなければいけない大事なポイントです!
撹拌Re数とは、あくまでも回転翼の先端近傍の流れを代表した無次元数であり、翼幅とか翼段数等の槽内全域の循環流に影響を与える因子を無視したものなのです。よって、同一形状の撹拌槽でサイズが異なる場合に無次元数として利用できる因子ではありますが、翼幅や段数が異なる形状の撹拌槽同士を撹拌Re数のみで比較・議論することは意味がないのです。
同じ翼形状のパドル翼でも1段と2段では全く異なる撹拌槽であるとの認識が必要なのです。一方、円管内のRe数では円形断面と言う意味では、どんな円管も幾何学的相似形が保たれているので、流れを示す指標として優等生なのです。

なるほど、図3のような「多段翼だけれど各段で翼径が異なる場合に、最も径の大きな段の翼径を代表長さとする」のも、流れへの影響が大きい箇所を便宜的に選定しているだけで、実際には槽内の上下で撹拌翼の径も先端速度も異なっているのだと言うことを理解しておく必要がありそうだね。
と言うことは、撹拌Re数が翼先端近傍の流れを代表しているのであれば、マックスブレンド®翼のような大型撹拌翼の場合は、翼先端部分が槽内上下方向に連続して存在するので、1段や2段の多段パドル翼に比べて槽内全域の流動状態を比較的良好に代表しているのかもしれないね。ふむふむ。
図3 翼径が異なる撹拌槽の代表長さ
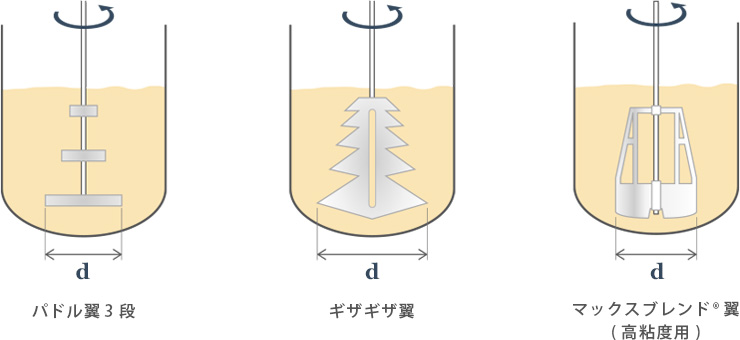

そうですね、マックスブレンド®翼のような大型翼はある意味、「無限段の多段パドル翼」とも言えますよね。マックスブレンド®翼でのスケールアップが従来の多段パドル翼よりもやり易いとの理由も、マックスブレンド®翼の撹拌Re数が槽内全域の流動を比較的良好に代表していることから来ているのかもしれませんね。
いかがでしたか?撹拌Re数の本質が、 なんとなくでも掴めてきたでしょうか。
撹拌Re数をよく理解することで、 道具として上手に付き合っていくことが大事です。
さて、 次回の講座では、 皆さんも興味深いであろう、 ラボ実験の結果を実機スケールで再現させる「スケールアップ」について、 基礎から分かりやすくご説明します。
- 撹拌講座 初級コース
-
- はじめに 撹拌の基礎用語
- その1 基礎の基礎、 撹拌を理解する3つのポイント
- その2 「撹拌の目的」の具体例
- その3 「粘り気」の単位が粘度
- その4 撹拌槽を巨大な粘度計と考えてみよう
- その5 動力変化で流れが見えますか(前編)
- その6 動力変化で流れが見えますか(後編)
- その7 撹拌Re数の本質を知ろう
- その8 スケールアップの基礎の基礎
- その9 スケールアップの基礎
- その10 撹拌槽の伝熱性能とは?
- その11 槽内側境膜伝熱係数hiとは?
- その12 撹拌講座の総括




