 Course 7
Learn the essence of the mixing Reynolds number
Course 7
Learn the essence of the mixing Reynolds number
In the last session and the session before the last, we explained that you can roughly expect the flow in a mixing vessel from the Reynolds number and the degree of power change. This time, take it easy and let us talk about what the mixing Reynolds number is, in the first place.
Originally, the Reynolds number is not a characteristic value specific to mixing, but an index widly applicable in the field of fluid dynamics, which is well known for the “Correlation diagram of fluid friction coefficient in circular pipe and Reynolds number”, which is used when estimating pressure loss in pipes or the like. In my school days, I was convinced that it was one of the last ten symbols to be used in social life, but in reality, it is a considerably important index.
In general, the Reynolds number is defined as follows:
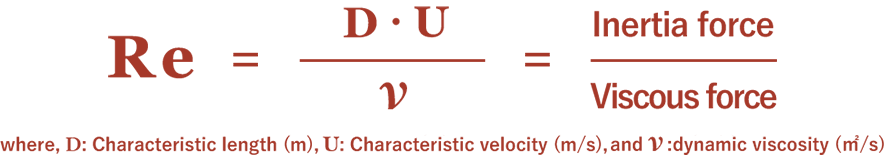
Oh, here come Dr.Nano and Max again! Dr.Nano asked two questions.

Dr.Nano
What does “characteristic” in “characteristic length” and “characteristic speed” in this equation mean? Isn’t it ambiguous?

Max
I’ve learned in the classroom that the word “characteristic” is used to indicated that the length, velocity, and others are those that are considered to be the most influential on the flow in the field of flow under consideration. In the case of a flow in a circular pipe, the characteristic length D is the inside diameter of the pipe, and the characteristic velocity U is the average flow rate in the pipe. I’ve also learned that the reason why the characteristic length is not the total length but the inside diameter of the pipe is because the friction resistance of the inner wall of the pipe greatly affects the flow.

I see. “Characteristic” means “most influential”, doesn’t it? Then, what is dynamic viscosity ν? What is the difference between ν and viscosity μ (Pa・s), which is often used in the field of mixing. It's troublesome, so why not just ordinary viscosity μ?

Oops, the difference between viscosity and dynamic viscosity? Well ... (watching the textbooks in his school days) the dynamic viscosity is defined as follows:
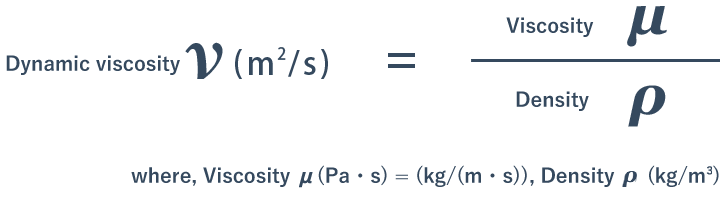

In the field of mixing, viscosity μ is a property of the target fluid, and is “an index of difficulty of moving objects in the fluid”. Whereas, the textbook says that dynamic viscosity ν is “an index of difficulty of moving the fluid itself”.
It also says that what affects the difficulty of movement of the fluid is density, and if the density is different, also the difficulty of moving the fluid (dynamic viscosity) is different even if the viscosity is the same.
Hmm. It seems hard to imagine.
As an example, assume an iron ball and a ping-pong ball having the same size coated with sticky oil in order to simulate two objects with the same size and the same viscosity μ (different only in weight). Although the surface viscosity is the same, the heavier (higher-density) iron ball is the easier to roll. Such a phenomenon seems to be evaluated as the easiness of movement (dynamic viscosity).
The reason why the dynamic viscosity is used to classify the grade of lubrication oil for gears and the like may be because the fluidity (easiness of dribbling) of the fluid clinging to the gears is evaluated.
Now, the definition of the Reynolds number in a broad sense is made clear, but Dr.Nano seems to still have some questions.

I see. I kind of understood dynamic viscosity, too. But, the form of the definition formula of the Reynolds number seems to be a little bit different between that in circular pipes and that for mixing...

That's right. As shown in Figure 1, the characteristic length and characteristic velocity of the Reynolds number are different between those in circular pipes and those for mixing.
Figure 1. Reynolds numbers in circular pipes and mixing
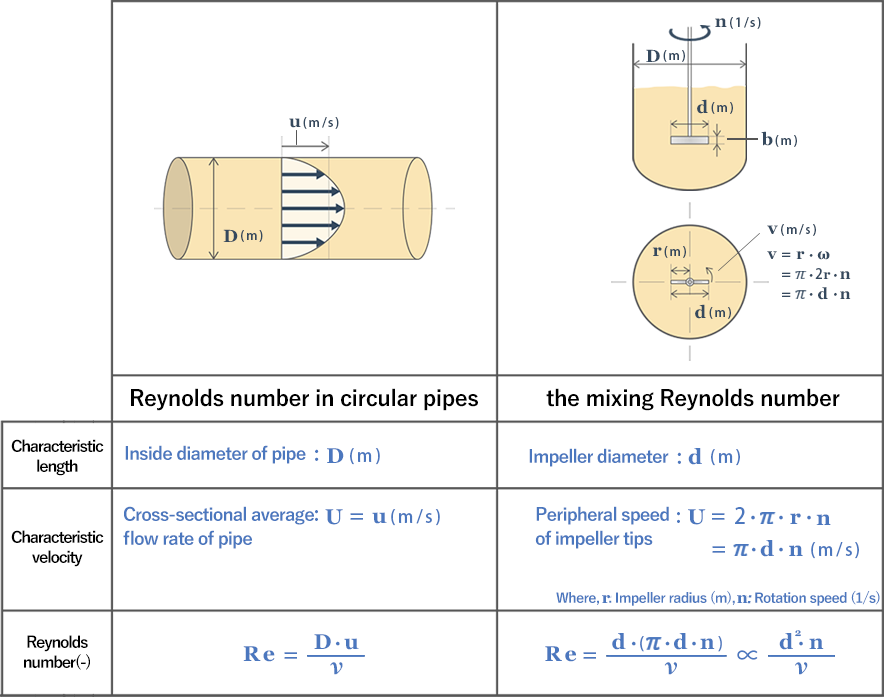

For the flow in a circular pipe, both the characteristic length and characteristic velocity seem to be selected relatively appropriately, but how for mixing? The characteristic length is the impeller diameter: d, and the characteristic velocity is the peripheral speed of impeller tips: U. It seems that the flow around the impeller tips is given more importance than that throughout the mixing vessel.

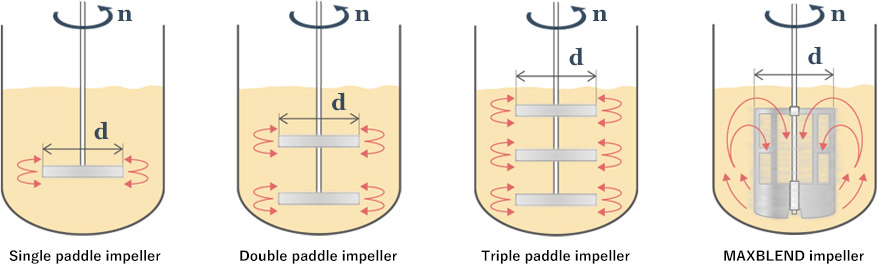
Exactly. Then, comparing the single, double, and triple paddle impellers, and also an large impeller like the MAXBLEND impeller as shown in Figure 2, the mixing Reynolds number must be the same among the four cases as long as they have the same impeller diameter and the same rotation speed. However, the actual liquid flow I saw on the spot was quite different. And also the consumption power is different among the four cases. I cannot persuade myself that the state of flow is the same among them...
Figure 2. Flow in vessel is different even with same Reynolds number

Yes! It is an important point that you need to be careful about when using the mixing Reynolds number!
The mixing Reynolds number is only a dimensionless number, which represents the flow around the tips of the rotating impeller and ignores the factors affecting the circulating flow throughout the vessel, such as the impeller width and the number of stages of impellers. Therefore, it is useful as a dimensionless factor when evaluating vessels with the same shape but different sizes, but it is no use comparing or discussing vessels having different impeller widths or numbers of stages of impellers by the mixing Reynolds number alone.
You have to be aware that a vessel with a single paddle impeller and a vessel with a double paddle impeller are quite different even the shape of the impeller is the same. Whereas, the Reynolds number in circular pipes is excellent as the index of flow because the cross-sections of circular pipes are always in a circular shape, and therefore geometrically similar.

Well, it looks like we need to be aware that taking the diameter of the largest impeller as the characteristic length for multi-stage impellers consisting of impellers with different diameters as shown in Figure 3 means evaluating only the parts greatly affecting the flow for the sake of convenience, but in reality, both the impeller diameter and the peripheral speed of impeller tips are different between the top and bottom of the vessel.
Considering the fact that the mixing Reynolds number represents the flow around impeller tips, it might represent the flow throughout the vessel relatively well in the case of using a large impeller such as the MAXBLEND impeller, which has tips continuously from the top to the bottom, compared to the cases of using a multi-stage paddle impeller. I got it.
Figure 3. Characteristic lengths of mixing vessels having multiple impeller diameters
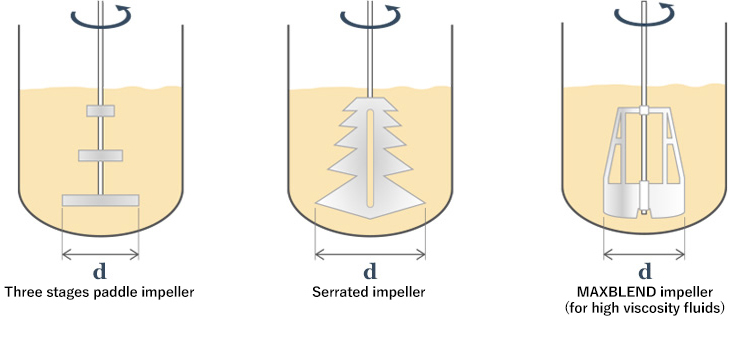

I agree. Large impellers such as the MAXBLEND impeller can be regarded as “infinite multi-stage paddle impellers” in a sense. Also the reason why it is easier to scale up when using the MAXBLEND impeller than when using a conventional multi-stage paddle impeller may be because the mixing Reynolds number of the MAXBLEND impeller represents the flow throughout the vessel relatively well.
How was this session? Can you somehow see the nature of the mixing Reynolds number?
It is important to use the mixing Reynolds number cleverly as a tool by understanding it well.
Then, in the next session, let us explain “scaling up”, which means the reproduction of the experimental results in the laboratory in the actual scale and which we believe you are interested in, from the basics in an easy-to-understand manner.
-
Mixing Course
Beginner
course -
- Introduction Basic terms of mixing
- Course 1 Basics of basics: Three points to understand mixing
- Course 2 Examples of the purposes of mixing
- Course 3 Viscosity is the unit of stickiness
- Course 4 Consider a mixing vessel as a huge viscometer
- Course 5 Can you see the flow from power change? (Part 1)
- Course 6 Can you see the flow from power change? (Part 2)
- Course 7 Learn the essence of the mixing Reynolds number
- Course 8 Basics of basics of scaling up
- Course 9 Basics of scaling up
- Course 10 What is heat transfer performance in a mixing vessel?
- Course 11 What is film heat transfer coefficient , hi?
- Course 12 Mixing course review
-
Mixing Course
Practical
course -
- Introduction Mixing course SEASON II
- Course 1 Immediately determine the basic specifications of the mixing vessel using three pieces of information: operating liquid volume, viscosity and density.
- Course 2 Find a plan to improve the productivity of the mixing tank on the existing production line! (Part 1)




